Young’s lattice and the RSK algorithm¶

This section provides some examples on Young’s lattice and the RSK (Robinson-Schensted-Knuth) algorithm explained in Chapter 8 of Stanley’s book [Stanley2013].

Young’s Lattice¶

We begin by creating the first few levels of Young’s lattice $Y$ . For this, we need to define the elements and the order relation for the poset, which is containment of partitions:

Sage

sage: level = 6
sage: elements = [b for n in range(level) for b in Partitions(n)]
sage: ord = lambda x,y: y.contains(x)
sage: Y = Poset((elements,ord), facade=True)
sage: H = Y.hasse_diagram()

Python

>>> from sage.all import *
>>> level = Integer(6)
>>> elements = [b for n in range(level) for b in Partitions(n)]
>>> ord = lambda x,y: y.contains(x)
>>> Y = Poset((elements,ord), facade=True)
>>> H = Y.hasse_diagram()

Sage Live

level = 6
elements = [b for n in range(level) for b in Partitions(n)]
ord = lambda x,y: y.contains(x)
Y = Poset((elements,ord), facade=True)
H = Y.hasse_diagram()

The resulting image looks best when dot2tex is installed:

Sage

sage: view(H)  # not tested

Python

>>> from sage.all import *
>>> view(H)  # not tested

Sage Live

view(H)  # not tested

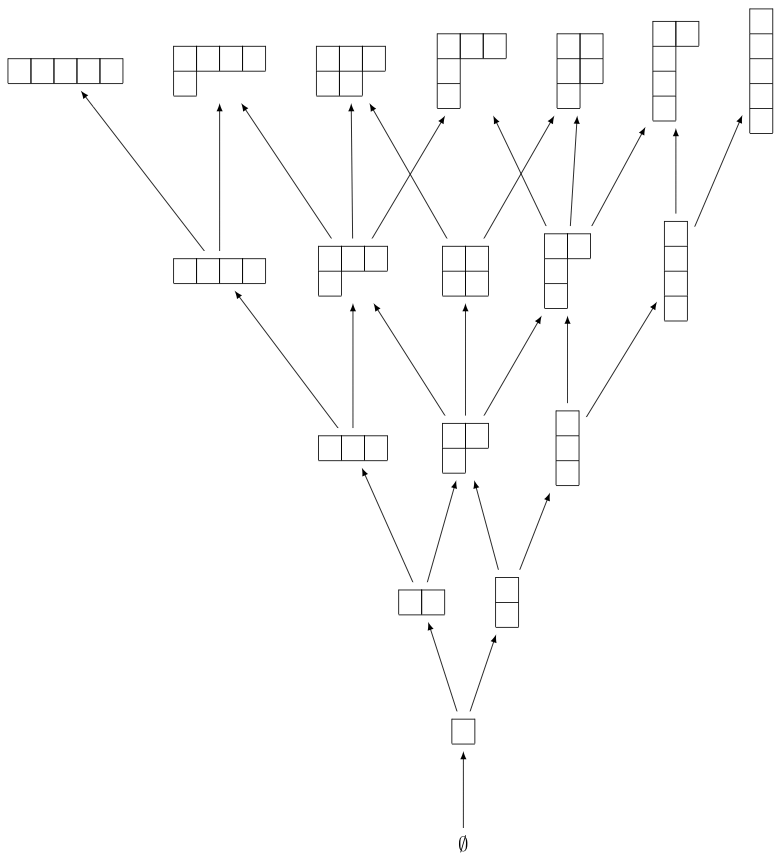
We can now define the up and down operators $U$ and $D$ on $Q Y$ . First we do so on partitions, which form a basis for $Q Y$ :

Sage

sage: QQY = CombinatorialFreeModule(QQ,elements)

sage: def U_on_basis(la):
....:     covers = Y.upper_covers(la)
....:     return QQY.sum_of_monomials(covers)

sage: def D_on_basis(la):
....:     covers = Y.lower_covers(la)
....:     return QQY.sum_of_monomials(covers)

Python

>>> from sage.all import *
>>> QQY = CombinatorialFreeModule(QQ,elements)

>>> def U_on_basis(la):
...     covers = Y.upper_covers(la)
...     return QQY.sum_of_monomials(covers)

>>> def D_on_basis(la):
...     covers = Y.lower_covers(la)
...     return QQY.sum_of_monomials(covers)

Sage Live

QQY = CombinatorialFreeModule(QQ,elements)
def U_on_basis(la):
    covers = Y.upper_covers(la)
    return QQY.sum_of_monomials(covers)
def D_on_basis(la):
    covers = Y.lower_covers(la)
    return QQY.sum_of_monomials(covers)

As a shorthand, one also can write the above as:

Sage

sage: U_on_basis = QQY.sum_of_monomials * Y.upper_covers
sage: D_on_basis = QQY.sum_of_monomials * Y.lower_covers

Python

>>> from sage.all import *
>>> U_on_basis = QQY.sum_of_monomials * Y.upper_covers
>>> D_on_basis = QQY.sum_of_monomials * Y.lower_covers

Sage Live

U_on_basis = QQY.sum_of_monomials * Y.upper_covers
D_on_basis = QQY.sum_of_monomials * Y.lower_covers

Here is the result when we apply the operators to the partition $(2, 1)$ :

Sage

sage: la = Partition([2,1])
sage: U_on_basis(la)
B[[2, 1, 1]] + B[[2, 2]] + B[[3, 1]]
sage: D_on_basis(la)
B[[1, 1]] + B[[2]]

Python

>>> from sage.all import *
>>> la = Partition([Integer(2),Integer(1)])
>>> U_on_basis(la)
B[[2, 1, 1]] + B[[2, 2]] + B[[3, 1]]
>>> D_on_basis(la)
B[[1, 1]] + B[[2]]

Sage Live

la = Partition([2,1])
U_on_basis(la)
D_on_basis(la)

Now we define the up and down operator on $Q Y$ :

Sage

sage: U = QQY.module_morphism(U_on_basis)
sage: D = QQY.module_morphism(D_on_basis)

Python

>>> from sage.all import *
>>> U = QQY.module_morphism(U_on_basis)
>>> D = QQY.module_morphism(D_on_basis)

Sage Live

U = QQY.module_morphism(U_on_basis)
D = QQY.module_morphism(D_on_basis)

We can check the identity $D_{i + 1} U_{i} - U_{i - 1} D_{i} = I_{i}$ explicitly on all partitions of $i = 3$ :

Sage

sage: for p in Partitions(3):
....:     b = QQY(p)
....:     assert D(U(b)) - U(D(b)) == b

Python

>>> from sage.all import *
>>> for p in Partitions(Integer(3)):
...     b = QQY(p)
...     assert D(U(b)) - U(D(b)) == b

Sage Live

for p in Partitions(3):
    b = QQY(p)
    assert D(U(b)) - U(D(b)) == b

We can also check that the coefficient of $λ ⊢ n$ in $U^{n} (\emptyset)$ is equal to the number of standard Young tableaux of shape $λ$ :

Sage

sage: u = QQY(Partition([]))
sage: for i in range(4):
....:     u = U(u)
sage: u
B[[1, 1, 1, 1]] + 3*B[[2, 1, 1]] + 2*B[[2, 2]] + 3*B[[3, 1]] + B[[4]]

Python

>>> from sage.all import *
>>> u = QQY(Partition([]))
>>> for i in range(Integer(4)):
...     u = U(u)
>>> u
B[[1, 1, 1, 1]] + 3*B[[2, 1, 1]] + 2*B[[2, 2]] + 3*B[[3, 1]] + B[[4]]

Sage Live

u = QQY(Partition([]))
for i in range(4):
    u = U(u)
u

For example, the number of standard Young tableaux of shape $(2, 1, 1)$ is $3$ :

Sage

sage: StandardTableaux([2,1,1]).cardinality()
3

Python

>>> from sage.all import *
>>> StandardTableaux([Integer(2),Integer(1),Integer(1)]).cardinality()
3

Sage Live

StandardTableaux([2,1,1]).cardinality()

We can test this in general:

Sage

sage: for la in u.support():
....:     assert u[la] == StandardTableaux(la).cardinality()

Python

>>> from sage.all import *
>>> for la in u.support():
...     assert u[la] == StandardTableaux(la).cardinality()

Sage Live

for la in u.support():
    assert u[la] == StandardTableaux(la).cardinality()

We can also check this against the hook length formula (Theorem 8.1):

Sage

sage: def hook_length_formula(p):
....:     n = p.size()
....:     return factorial(n) // prod(p.hook_length(*c) for c in p.cells())

sage: for la in u.support():
....:     assert u[la] == hook_length_formula(la)

Python

>>> from sage.all import *
>>> def hook_length_formula(p):
...     n = p.size()
...     return factorial(n) // prod(p.hook_length(*c) for c in p.cells())

>>> for la in u.support():
...     assert u[la] == hook_length_formula(la)

Sage Live

def hook_length_formula(p):
    n = p.size()
    return factorial(n) // prod(p.hook_length(*c) for c in p.cells())
for la in u.support():
    assert u[la] == hook_length_formula(la)

RSK Algorithm¶

Let us now turn to the RSK algorithm. We can verify Example 8.12 as follows:

Sage

sage: p = Permutation([4,2,7,3,6,1,5])
sage: RSK(p)
[[[1, 3, 5], [2, 6], [4, 7]], [[1, 3, 5], [2, 4], [6, 7]]]

Python

>>> from sage.all import *
>>> p = Permutation([Integer(4),Integer(2),Integer(7),Integer(3),Integer(6),Integer(1),Integer(5)])
>>> RSK(p)
[[[1, 3, 5], [2, 6], [4, 7]], [[1, 3, 5], [2, 4], [6, 7]]]

Sage Live

p = Permutation([4,2,7,3,6,1,5])
RSK(p)

The tableaux can also be displayed as tableaux:

Sage

sage: P,Q = RSK(p)
sage: P.pp()
1  3  5
2  6
4  7
sage: Q.pp()
1  3  5
2  4
6  7

Python

>>> from sage.all import *
>>> P,Q = RSK(p)
>>> P.pp()
1  3  5
2  6
4  7
>>> Q.pp()
1  3  5
2  4
6  7

Sage Live

P,Q = RSK(p)
P.pp()
Q.pp()

The inverse RSK algorithm is implemented as follows:

Sage

sage: RSK_inverse(P,Q, output='permutation')
[4, 2, 7, 3, 6, 1, 5]

Python

>>> from sage.all import *
>>> RSK_inverse(P,Q, output='permutation')
[4, 2, 7, 3, 6, 1, 5]

Sage Live

RSK_inverse(P,Q, output='permutation')

We can verify that the RSK algorithm is a bijection:

Sage

sage: def check_RSK(n):
....:     for p in Permutations(n):
....:          assert RSK_inverse(*RSK(p), output='permutation') == p
sage: for n in range(5):
....:     check_RSK(n)

Python

>>> from sage.all import *
>>> def check_RSK(n):
...     for p in Permutations(n):
...          assert RSK_inverse(*RSK(p), output='permutation') == p
>>> for n in range(Integer(5)):
...     check_RSK(n)

Sage Live

def check_RSK(n):
    for p in Permutations(n):
         assert RSK_inverse(*RSK(p), output='permutation') == p
for n in range(5):
    check_RSK(n)