Elementary crystals¶
Note
Each of these crystals will work with any Cartan matrix input (with weights from the weight lattice corresponding to the Cartan matrix given).
T-crystal¶
Let
The crystal
sage: B = crystals.Tableaux(['A',2],shape=[2,1])
sage: T = crystals.elementary.T(['A',2], B.Lambda()[1] + B.Lambda()[2])
sage: V = crystals.TensorProduct(T,B)
sage: for x in V:
....: print(x.weight())
....:
(4, 2, 0)
(3, 3, 0)
(3, 2, 1)
(3, 1, 2)
(2, 2, 2)
(4, 1, 1)
(3, 2, 1)
(2, 3, 1)
sage: for x in B:
....: print(x.weight() + T[0].weight())
....:
(4, 2, 0)
(3, 3, 0)
(3, 2, 1)
(3, 1, 2)
(2, 2, 2)
(4, 1, 1)
(3, 2, 1)
(2, 3, 1)
Warning
Sage uses the opposite convention for the tensor product rule to Kashiwara’s definition, so care must be taken when comparing the examples here with Kashiwara’s papers.
Here is an example using a hyperbolic Cartan matrix:
sage: A = CartanMatrix([[2,-4],[-4,2]])
sage: La = RootSystem(A).weight_lattice().fundamental_weights()
sage: La
Finite family {0: Lambda[0], 1: Lambda[1]}
sage: T = crystals.elementary.T(A,La[1])
sage: T
The T crystal of type [ 2 -4]
[-4 2] and weight Lambda[1]
C-crystal¶
Defined in [Kashiwara1993], the component crystal
Note
The crystal
sage: P = RootSystem("C2").weight_lattice()
sage: La = P.fundamental_weights()
sage: h = P.simple_coroots()
sage: T = crystals.elementary.T("C2", 2*La[1])
sage: C = crystals.elementary.Component(P)
sage: B = crystals.TensorProduct(C,T)
sage: b = B(C[0],T[0])
sage: for i in B.index_set(): print(b.epsilon(i))
-2
0
sage: for i in B.index_set(): print(b.phi(i))
0
0
sage: for i in B.index_set(): print(b.f(i))
None
None
sage: for i in B.index_set(): print(b.e(i))
None
None
This new crystal can be summarized into the R-crystal below.
R-crystal¶
For a fixed weight
where
Tensoring
Warning
Sage uses the opposite convention for the tensor product rule to Kashiwara’s definition, so care must be taken when comparing the examples here with some of the literature.
For example, suppose
sage: La = RootSystem(['B',4]).weight_lattice().fundamental_weights()
sage: Bla = crystals.NakajimaMonomials(['B',4], La[1]+La[2])
sage: Bmu = crystals.NakajimaMonomials(['B',4], La[1])
sage: R = crystals.elementary.R(['B',4], -La[2])
sage: T = crystals.TensorProduct(R,Bla)
sage: mg = mg = T(R[0], Bla.module_generators[0])
sage: S = T.subcrystal(generators=[mg])
sage: G = T.digraph(subset=S)
sage: Bmu.digraph().is_isomorphic(G, edge_labels=True)
True
sage: view(G, tightpage=True) # optional - dot2tex graphviz, not tested (opens external window)
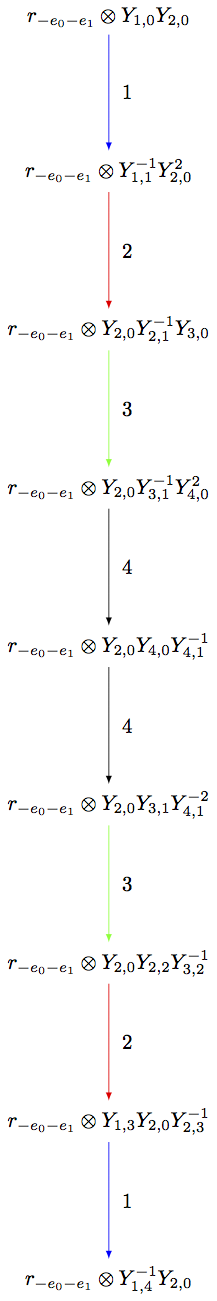
For
where the crystal structure is given by
See [Kashiwara1993] or [Kashiwara1995] for more information. Here is an example:
sage: B = crystals.elementary.Elementary("A2",1)
sage: S = B.subcrystal(max_depth=4, generators=[B(0)])
sage: sorted(s for s in S)
[-4, -3, -2, -1, 0, 1, 2, 3, 4]
sage: G = B.digraph(subset=S)
sage: view(G, tightpage=True) # optional - dot2tex graphviz, not tested (opens external window)
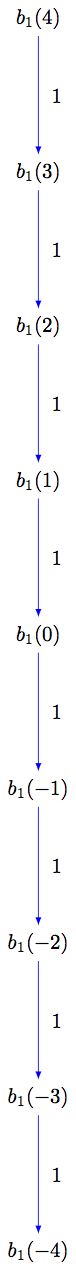
Warning
To reiterate, Sage uses the opposite convention for the tensor product rule
to Kashiwara’s definition. In particular, using Sage’s convention, one has